rust_practice_leetcode_daily_code2

fn main(){

}

fn main(){

}

fn main(){

}

fn main(){

}

主要需要根据题目得出

/// 0 = num1 - 2^i - num2; /// num1 - k * num2 = k * 2^i

这个公式..

然后文字描述

===>> 就是num1 - k次操作的数 num1 - k * num2 = k * 2^i ( k 个 2次幂的和，因为 i 不一定是一样的. )

我们可以得到 num1 - k * num2 === s

即判断 s 是不是可以被表示成 k 个 2次幂 的和 --- 可以就是返回k，不可以返回 -1

k 从 1(0也可以) 到 60 遍历 == 计算

AC Code

#![allow(dead_code)]
#![allow(unused_attributes)]
#![allow(unused_variables)]


fn main() {
    println!("Hello, world!");
}

struct Solution {}

/**
给你两个整数：num1 和 num2 。
在一步操作中，你需要从范围 [0, 60] 中选出一个整数 i ，并从 num1 减去 2^i + num2 。
请你计算，要想使 num1 等于 0 需要执行的最少操作数，并以整数形式返回。
如果无法使 num1 等于 0 ，返回 -1 。


示例 1：
输入：num1 = 3, num2 = -2
输出：3
解释：可以执行下述步骤使 3 等于 0 ：
- 选择 i = 2 ，并从 3 减去 22 + (-2) ，num1 = 3 - (4 + (-2)) = 1 。
- 选择 i = 2 ，并从 1 减去 22 + (-2) ，num1 = 1 - (4 + (-2)) = -1 。
- 选择 i = 0 ，并从 -1 减去 20 + (-2) ，num1 = (-1) - (1 + (-2)) = 0 。
可以证明 3 是需要执行的最少操作数。


示例 2：
输入：num1 = 5, num2 = 7
输出：-1
解释：可以证明，执行操作无法使 5 等于 0 。
 

提示：
1 <= num1 <= 10^9
-10^9 <= num2 <= 10^9
*
*/


/// 0 = num1 - 2^i - num2;
/// num1 - k * num2 = k * 2^i
impl Solution {
    pub fn make_the_integer_zero(num1: i32, num2: i32) -> i32 {
        let a = num1 as i64;
        let b = num2 as i64;

        for k in 1..=60 {
            let s = a - k * b;

            if s <= 0 {
                continue ;
            }

            // 检查剩余值 S 是否可以表示成 k 个 2的幂次的和(2^i)
            // 1. s的二进制中1的个数不超过 k (每个1可以对应一个k)
            // 2. s >=k (最小的k个 2^0 的和就是 k )
            if s.count_ones() as i64 <= k as i64 && s >= k {
                return k as i32;
            }
        }
        

        // 遍历完 k 后未找到解.
        -1
    }
}

方法思路 要解决这个问题，我们需要找到所有满足条件的点对 (A, B)， 其中 A 位于 B 的左上角（即 A 的 x 坐标小于等于 B 的 x 坐标，且 A 的 y 坐标大于等于 B 的 y 坐标）， 并且由 A 和 B 形成的长方形（可能退化为一条直线）内部或边上没有其他点。

具体步骤如下：

遍历所有点对：对于每一个点作为 A，检查其他点是否可以作为 B。

验证左上角条件：确保 A 的 x 坐标不大于 B 的 x 坐标，且 A 的 y 坐标不小于 B 的 y 坐标。

检查中间点：对于符合条件的点对 (A, B)，检查是否在由 A 和 B 形成的长方形内部或边上存在其他点。 如果有，则该点对不合法。

统计合法点对：统计所有满足条件的点对数量。

AC Code

#![allow(dead_code)]
#![allow(unused_attributes)]
#![allow(unused_variables)]


fn main() {
    println!("Hello, world!");
}

struct Solution {}

/**
 
给你一个  n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [xi, yi] 。


计算点对 (A, B) 的数量，其中
A 在 B 的左上角，并且
它们形成的长方形中（或直线上）没有其它点（包括边界）。
返回数量。

[1,1]
[2,2]
[3,3]
示例 1：
输入：points = [[1,1],[2,2],[3,3]]
输出：0
解释：
没有办法选择 A 和 B，使得 A 在 B 的左上角。


[6,2]
[4,4]
[2,6]
示例 2：
输入：points = [[6,2],[4,4],[2,6]]
输出：2
解释：
左边的是点对 (points[1], points[0])，其中 points[1] 在 points[0] 的左上角，并且形成的长方形内部是空的。
中间的是点对 (points[2], points[1])，和左边的一样是合法的点对。
右边的是点对 (points[2], points[0])，其中 points[2] 在 points[0] 的左上角，
但 points[1] 在长方形内部，所以不是一个合法的点对。


[3,1]
[1,3]
[1,1]
示例 3：
输入：points = [[3,1],[1,3],[1,1]]
输出：2
解释：
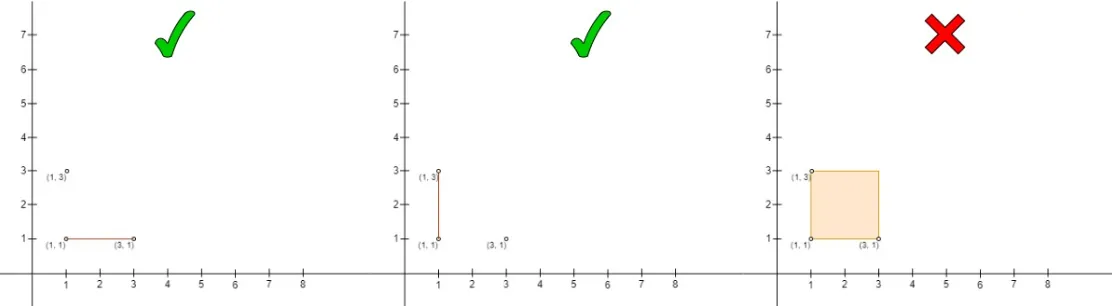
左边的是点对 (points[2], points[0])，其中 points[2] 在 points[0] 的左上角并且在它们形成的直线上没有其它点。
注意两个点形成一条线的情况是合法的。

中间的是点对 (points[1], points[2])，和左边一样也是合法的点对。
右边的是点对 (points[1], points[0])，它不是合法的点对，因为 points[2] 在长方形的边上。
 

提示：
2 <= n <= 50
points[i].length == 2
0 <= points[i][0], points[i][1] <= 50
points[i] 点对两两不同。
 *
 */

impl Solution {
    // 暴力解法...遍历每个点作为A、作为B，然后再遍历是否有点在A、B形成的区域内.
    pub fn number_of_pairs(points: Vec<Vec<i32>>) -> i32 {
        let len = points.len();
        let mut ans = 0;

        for i in 0..len {
            for j in 0..len {
                if i == j {
                    continue;
                }

                // 获取A、B
                let a = &points[i];
                let b = &points[j];

                // 直线也算..参考给出的示例3
                if a[0] <= b[0] && a[1] >= b[1] {
                    
                    let mut exist = false;

                    for k in 0..len {
                        if k == i || k == j {
                            continue ;
                        }

                        let other = &points[k];

                        if other[0] >= a[0] && other[0] <= b[0] && other[1] <= a[1] && other[1] >= b[1] {
                            exist = true;
                            break ;
                        }
                    }

                    if !exist {
                        ans += 1;
                    }
                }
            }
        }

        ans
    }
}

#![allow(dead_code)]
#![allow(unused_attributes)]
#![allow(unused_variables)]


fn main() {
    println!("Hello, world!");
}

struct Solution {}

/**
 
给你三个整数 x、y 和 z，表示数轴上三个人的位置：

x 是第 1 个人的位置。
y 是第 2 个人的位置。
z 是第 3 个人的位置，第 3 个人 不会移动 。
第 1 个人和第 2 个人以 相同 的速度向第 3 个人移动。

判断谁会 先 到达第 3 个人的位置：

如果第 1 个人先到达，返回 1 。
如果第 2 个人先到达，返回 2 。
如果两个人同时到达，返回 0 。
根据上述规则返回结果。

 

示例 1：
输入： x = 2, y = 7, z = 4
输出： 1
解释：
第 1 个人在位置 2，到达第 3 个人（位置 4）需要 2 步。
第 2 个人在位置 7，到达第 3 个人需要 3 步。
由于第 1 个人先到达，所以输出为 1。

示例 2：
输入： x = 2, y = 5, z = 6
输出： 2
解释：
第 1 个人在位置 2，到达第 3 个人（位置 6）需要 4 步。
第 2 个人在位置 5，到达第 3 个人需要 1 步。
由于第 2 个人先到达，所以输出为 2。

示例 3：
输入： x = 1, y = 5, z = 3
输出： 0
解释：
第 1 个人在位置 1，到达第 3 个人（位置 3）需要 2 步。
第 2 个人在位置 5，到达第 3 个人需要 2 步。
由于两个人同时到达，所以输出为 0。


提示：
1 <= x, y, z <= 100
 *
 */

impl Solution {
    pub fn find_closest(x: i32, y: i32, z: i32) -> i32 {
        let a = (x - z).abs();
        let b = (y - z) .abs();

        if a < b {
            1
        } else if a > b {
            2 
        } else {
            0
        }
    }
}

找出对角线i+j=k，0..row+col-2，然后枚举对角线..

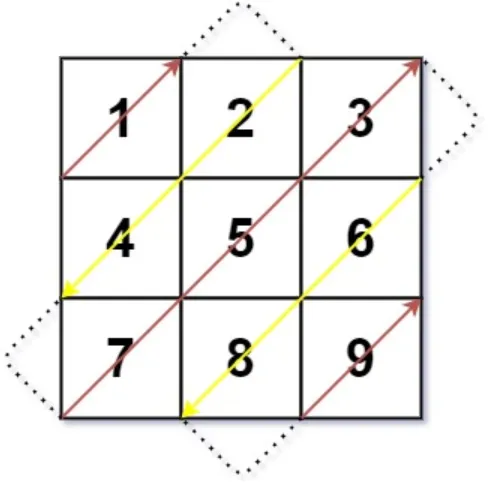
对于每条对角线，行号 i 加列号 j 是一个定值。示例 1 正中间对角线的 i+j 恒为 2。（可以回想一下 51. N 皇后 的写法）

设 k=i+j，那么左上角那条对角线的 k=0，右下角那条对角线的 k=(m−1)+(n−1)=m+n−2。

枚举 k=0,1,2,…,m+n−2，就相当于在从左上到右下，一条一条地枚举对角线。

由于 i+j=k，知道 j 就知道 i，所以我们只需要计算出每条对角线的 j 的最小值和最大值，就可以开始遍历对角线了。

由于 j=k−i，当 i=m−1 时 j 取到最小值 k−m+1，但这个数不能是负数，所以最小的 j 是 max(k−m+1,0)。
由于 j=k−i，当 i=0 时 j 取到最大值 k，但这个数不能超过 n−1，所以最大的 j 是 min(k,n−1)。
然后就可以模拟了：

枚举 k=0,1,2,…,m+n−2。
如果 k 是偶数，我们从小到大枚举 j，否则从大到小枚举 j。其中 j 的范围是 [max(k−m+1,0),min(k,n−1)]。
把 mat[k−j][j] 加入答案。

AC Code

#![allow(dead_code)]
#![allow(unused_attributes)]
#![allow(unused_variables)]

fn main() {
    println!("Hello, world!");
}

struct Solution {}

/**
*

给你一个大小为 m x n 的矩阵 mat ，
请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

[1, 2 ,3]
[4, 5, 6]
[7, 8, 9]
示例 1：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]


[1, 2]
[3, 4]
示例 2：
输入：mat = [[1,2],[3,4]]
输出：[1,2,3,4]
 

提示：
m == mat.length
n == mat[i].length
1 <= m, n <= 10^4
1 <= m * n <= 10^4
-10^5 <= mat[i][j] <= 10^5

*
*/

impl Solution {

    pub fn find_diagonal_order(mat: Vec<Vec<i32>>) -> Vec<i32> {
        let row = mat.len();
        let col = mat[0].len();

        // 分配空间
        let mut ans = Vec::with_capacity(row * col);

        // 横坐标 + 纵坐标 = row - 1 + (row - 1) = row + col - 2
        for k in 0..=(row + col - 2) {
            // 最小的列、最大的列
            // 知道 列 之后，就知道 行了. i + j = k ,  i = k - j
            // j 取最小值，即 j = k - i, i 最大 row -1
            // j 取最大值，即 j= k - i, i = 0, k <= col - 1
            let min_j = k.saturating_sub(row - 1);
            let max_j = k.min(col - 1);

            if k % 2 == 0 {
                // 从左到右
                for j in min_j..=max_j {
                    ans.push(mat[k - j][j]);
                }
            } else {
                // 从右到左
                for j in (min_j..=max_j).rev() {
                    ans.push(mat[k - j][j]);
                }
            }

        }

        ans
    }
}

每个矩形的对角线长度可以通过勾股定理计算

长的平方 + 宽的平方 开根号.. 这道题可以不用开根号.

AC Code

#![allow(dead_code)]
#![allow(unused_attributes)]
#![allow(unused_variables)]

fn main() {
    println!("Hello, world!");
}

struct Solution {}

/**
*

给你一个下标从 0 开始的二维整数数组 dimensions。

对于所有下标 i（0 <= i < dimensions.length），dimensions[i][0] 表示矩形 i 的长度，
而 dimensions[i][1] 表示矩形 i 的宽度。

返回对角线最 长 的矩形的 面积 。如果存在多个对角线长度相同的矩形，返回面积最 大 的矩形的面积。

 

示例 1：
输入：dimensions = [[9,3],[8,6]]
输出：48
解释：
下标 = 0，长度 = 9，宽度 = 3。对角线长度 = sqrt(9 * 9 + 3 * 3) = sqrt(90) ≈ 9.487。
下标 = 1，长度 = 8，宽度 = 6。对角线长度 = sqrt(8 * 8 + 6 * 6) = sqrt(100) = 10。
因此，下标为 1 的矩形对角线更长，所以返回面积 = 8 * 6 = 48。


示例 2：
输入：dimensions = [[3,4],[4,3]]
输出：12
解释：两个矩形的对角线长度相同，为 5，所以最大面积 = 12。
 

提示：
1 <= dimensions.length <= 100
dimensions[i].length == 2
1 <= dimensions[i][0], dimensions[i][1] <= 100

*
*/

impl Solution {
    pub fn area_of_max_diagonal(dimensions: Vec<Vec<i32>>) -> i32 {
        
        // 最长的对角线
        let mut max_duijiao = 0;
        // 最大的矩形面积
        let mut max_area = 0;

        for di in dimensions {
            let a = di[0];
            let b = di[1];

            let temp_duijiao = a*a + b*b;
            let temp_area = a * b;

            if temp_duijiao > max_duijiao {
                max_area = temp_area;
                max_duijiao = temp_duijiao;
            } else if temp_duijiao == max_duijiao {

                // 更新最大面积
                max_area = max_area.max(temp_area);                
            }

        }

        max_area
    }
}

问题特性：需要尝试所有数字的排列组合、运算符选择和括号组合（运算顺序）。

解空间明确：每一步的选择（数字、运算符）是有限的，适合系统性地枚举。

回溯的本质 ====> 暴力穷举所有可能性

通过递归尝试每一种可能的运算路径，并在发现当前路径无法达到目标时回退（撤销选择），尝试其他路径。

带注释版本

impl Solution {
    pub fn judge_point24(cards: Vec<i32>) -> bool {
        // 将整数转换为浮点数，便于进行实数除法
        let mut nums: Vec<f64> = cards.into_iter().map(|x| x as f64).collect();
        Self::dfs(&mut nums)
    }

    // 深度优先搜索，尝试所有可能的运算组合
    fn dfs(nums: &mut Vec<f64>) -> bool {
        // 如果只剩一个数字，检查是否接近24
        if nums.len() == 1 {
            return (nums[0] - 24.0).abs() < 1e-6;
        }

        // 遍历所有不同的数字对
        for i in 0..nums.len() {
            for j in 0..nums.len() {
                if i == j {
                    continue; // 跳过相同的数字
                }

                // 创建一个新列表，包含未被选中的数字
                let mut new_nums: Vec<f64> = nums.iter().enumerate()
                    .filter(|&(k, _)| k != i && k != j)
                    .map(|(_, &num)| num)
                    .collect();

                // 尝试四种运算符
                let ops = [|a, b| a + b, |a, b| a - b, |a, b| a * b, |a, b| a / b];
                for op in ops.iter() {
                    // 处理除法时除数不能为零的情况
                    if *op == ops[3] && nums[j].abs() < 1e-6 {
                        continue;
                    }
                    // 将运算结果加入新列表
                    new_nums.push(op(nums[i], nums[j]));
                    // 递归检查是否能得到24
                    if Self::dfs(&mut new_nums) {
                        return true;
                    }
                    // 回溯，移除运算结果
                    new_nums.pop();
                }
            }
        }
        false
    }
}

AC Code

#![allow(dead_code)]
#![allow(unused_attributes)]
#![allow(unused_variables)]

fn main() {
    let s = String::from("value");

    let strs = first_word(&s);
    println!("{strs:?}");

    println!("Hello, world!");
}

struct Solution {}

/**
 *

给定一个长度为4的整数数组 cards 。
你有 4 张卡片，每张卡片上都包含一个范围在 [1,9] 的数字。
您应该使用运算符 ['+', '-', '*', '/'] 和括号 '(' 和 ')' 将这些卡片上的数字排列成数学表达式，
以获得值24。

你须遵守以下规则:
除法运算符 '/' 表示实数除法，而不是整数除法。
    例如， 4 /(1 - 2 / 3)= 4 /(1 / 3)= 12 。

每个运算都在两个数字之间。特别是，不能使用 “-” 作为一元运算符。
    例如，如果 cards =[1,1,1,1] ，则表达式 “-1 -1 -1 -1” 是 不允许 的。

你不能把数字串在一起
    例如，如果 cards =[1,2,1,2] ，则表达式 “12 + 12” 无效。

如果可以得到这样的表达式，其计算结果为 24 ，则返回 true ，否则返回 false 。



示例 1:
输入: cards = [4, 1, 8, 7]
输出: true
解释: (8-4) * (7-1) = 24


示例 2:
输入: cards = [1, 2, 1, 2]
输出: false

提示:
cards.length == 4
1 <= cards[i] <= 9

 *
 */

impl Solution {
    pub fn judge_point24(cards: Vec<i32>) -> bool {
        let mut nums: Vec<f64> = cards.into_iter().map(|x| x as f64).collect();

        Self::dfs(&mut nums)
    }

    // 不断将两个数合成一个数，直到最后一个的时候，判断是否接近 24
    fn dfs(nums: &mut Vec<f64>) -> bool {
        if nums.len() == 1 {
            return (nums[0] - 24.0).abs() < 1e-6;
        }

        // 双重循环遍历 --- 拿两个数进行 合成 -- 一个新的数
        for i in 0..nums.len() {
            for j in 0..nums.len() {
                if i == j {
                    continue;
                }

                // 创建合成之后的 新数字列表 -- 排除拿的两个数
                let mut new_nums: Vec<f64> = nums
                    .iter()
                    .enumerate() // (index, item)
                    .filter(|&(k, _)| k != i && k != j)
                    .map(|(_, &num)| num)
                    .collect();


                // 四种运算符
                let ops: [fn(f64, f64) -> f64; 4] = [
                    |a, b| a + b,
                    |a, b| a - b,
                    |a, b| a * b,
                    |a, b| a / b,
                ];


                for op in ops.iter() {
                    if *op == ops[3] && nums[j].abs() < 1e-6 {
                        continue;
                    }

                    let new_n = op(nums[i], nums[j]);
                    new_nums.push(new_n);

                    if Self::dfs(&mut new_nums) {
                        return true;
                    }

                    // 回滚
                    new_nums.pop();
                }   

            }
        }

        false
    }

    
}

另一种 实现， 匿名函数数组换成 枚举 的实现

impl Solution {
    pub fn judge_point24(cards: Vec<i32>) -> bool {
        let mut nums: Vec<f64> = cards.into_iter().map(|x| x as f64).collect();

        Self::dfs(&mut nums)
    }

    // 不断将两个数合成一个数，直到最后一个的时候，判断是否接近 24
    fn dfs(nums: &mut Vec<f64>) -> bool {
        if nums.len() == 1 {
            return (nums[0] - 24.0).abs() < 1e-6;
        }

        // 四种运算符
        #[derive(PartialEq)] // 解决binary operation `==` cannot be applied to type `Op` 
        enum Op {
            Add,
            Sub,
            Mul,
            Div,
        }

        let ops = [Op::Add, Op::Sub, Op::Mul, Op::Div];

        // 双重循环遍历 --- 拿两个数进行 合成 -- 一个新的数
        for i in 0..nums.len() {
            for j in 0..nums.len() {
                if i == j {
                    continue;
                }

                // 创建合成之后的 新数字列表 -- 排除拿的两个数
                let mut new_nums: Vec<f64> = nums
                    .iter()
                    .enumerate() // (index, item)
                    .filter(|&(k, _)| k != i && k != j)
                    .map(|(_, &num)| num)
                    .collect();

                for op in &ops {
                    if *op == Op::Div && nums[j].abs() < 1e-6 {
                        continue;
                    }

                    let new_n = match op {
                        Op::Add => nums[i] + nums[j],
                        Op::Sub => nums[i] - nums[j],
                        Op::Mul => nums[i] * nums[j],
                        Op::Div => nums[i] / nums[j],
                    };
                    new_nums.push(new_n);

                    if Self::dfs(&mut new_nums) {
                        return true;
                    }

                    // 回滚
                    new_nums.pop();
                }
            }
        }

        false
    }
}

固定长度的数组（如 [u8; 10]）可以直接用 == 比较

统计 n 的数字频率
将 n 转为字符串，遍历每个字符，统计 0-9 的出现次数。
例如：n = 46 → "46" → 4:1, 6:1, 其余:0。


生成所有可能的 2 的幂的数字频率
计算 1, 2, 4, 8, 16, ..., 2^30 的数字频率，并存储（如 HashSet）。



比较数字频率
检查 n 的数字频率是否在 2 的幂的频率集合中。

AC Code

#![allow(unused_variables)]
#![allow(dead_code)]



/**
 *
给定正整数 n ，我们按任何顺序（包括原始顺序）将数字重新排序，注意其前导数字不能为零。

如果我们可以通过上述方式得到 2 的幂，返回 true；否则，返回 false。

 
示例 1：
输入：n = 1
输出：true


示例 2：
输入：n = 10
输出：false
 

提示：
1 <= n <= 10^9
*
*/
struct Solution {}

impl Solution {
    pub fn reordered_power_of2(n: i32) -> bool {
        let dig = n.to_string();

        let len = dig.len();
        // 数字频率
        let count_target = Self::count_num(n);

        let mut power = 1;

        let er_ci_mi_max = 30;
        for _ in 0..er_ci_mi_max {
            let dig_len = power.to_string();

            if dig_len.len() == len {
                // 长度一样的时候，比较频率
                
                let count_current = Self::count_num(power);
                
                if count_current == count_target {
                    return true;
                }
            } else if dig_len.len() > len {
                return false;
            }

            power *= 2;
        }

        false
    }

    fn count_num(n: i32) -> [u8; 10] {
        let mut count = [0; 10];
        
        for i in n.to_string().chars() {
            let d = i.to_digit(10).unwrap() as usize;

            count[d] += 1; 
        }

        count
    }
}

根据分析，当 n ≥ 5000 时，A 先空的概率会趋近于 1（误差 < 1e-5），所以直接返回 1.0。

🚩边界条件定义如下：
状态	返回值	原因
A ≤ 0 且 B > 0	1.0	A 先空了，B 还没空，完全满足题意
A ≤ 0 且 B ≤ 0	0.5	A 和 B 同时空了，计为“0.5”
A > 0 且 B ≤ 0	0.0	B 先空了，不满足题意，不计入

这些返回值直接对应题目描述中这个定义：
    返回“汤 A 在 B 前耗尽的概率，加上两种汤在 同一回合 耗尽概率的一半”。



假如你有 50ml 的 A 和 B，然后第一次操作是四种之一（等概率 0.25）：

op1：A=0, B=50 ⇒ A 先空 ⇒ 返回 1.0
op2：A=0, B=25 ⇒ A 先空 ⇒ 返回 1.0
op3：A=0, B=0 ⇒ 同时空 ⇒ 返回 0.5
op4：A=25, B=0 ⇒ B 先空 ⇒ 返回 0.0

那么这次 DFS 的期望结果就是：
0.25 × (1.0 + 1.0 + 0.5 + 0.0) = 0.625

这正是题目的示例输出

🔬 2. 为什么 n 越大概率越趋近于 1
在模拟 dfs(n, n) 的过程中，我们要不断进行分支计算。

越往后（A、B 越少），越可能先把 A 倒空，或 A 和 B 同时倒空。

B 先空的概率逐渐趋近于 0，因为大多数操作都是“对 A 伤害更大”。

可以理解为：A 几乎总是比 B 更容易被先倒完。


经验模拟结论
刷题过程中，有人统计了如下表格（部分）：

| n    | 概率 P(n)     | 与 1 的差值  |
| ---- | ----------- | -------- |
| 100  | 0.71875     | 0.28125  |
| 500  | 0.96875     | 0.03125  |
| 1000 | 0.99609     | 0.00391  |
| 2000 | 0.99994     | 0.00006  |
| 5000 | 0.99999xxxx | < 1e-5 ✅ |


你会发现：

从 n = 2000 开始，结果就已经非常接近 1 了。

n = 5000 时，B 先空的概率已经小到可以忽略了（< 0.00001）。

AC Code

#![allow(unused_variables)]
#![allow(dead_code)]

use std::collections::HashMap;


/**
 *
你有两种汤，A 和 B，每种初始为 n 毫升。在每一轮中，会随机选择以下四种服务操作中的一种，
每种操作的概率为 0.25，且与之前的所有轮次 无关：

从汤 A 取 100 毫升，从汤 B 取 0 毫升
从汤 A 取 75 毫升，从汤 B 取 25 毫升
从汤 A 取 50 毫升，从汤 B 取 50 毫升
从汤 A 取 25 毫升，从汤 B 取 75 毫升

注意：
不存在先分配 100 ml 汤B 的操作。
汤 A 和 B 在每次操作中同时被倒入。
如果一次操作要求你倒出比剩余的汤更多的量，请倒出该汤剩余的所有部分。
操作过程在任何回合中任一汤被用完后立即停止。

返回汤 A 在 B 前耗尽的概率，加上两种汤在 同一回合 耗尽概率的一半。
返回值在正确答案 10^-5 的范围内将被认为是正确的。



示例 1:
输入：n = 50
输出：0.62500
解释：
如果我们选择前两个操作，A 首先将变为空。
对于第三个操作，A 和 B 会同时变为空。
对于第四个操作，B 首先将变为空。
所以 A 变为空的总概率加上 A 和 B 同时变为空的概率的一半是 0.25 *(1 + 1 + 0.5 + 0)= 0.625。


示例 2:
输入：n = 100
输出：0.71875
解释：
如果我们选择第一个操作，A 首先将变为空。
如果我们选择第二个操作，A 将在执行操作 [1, 2, 3] 时变为空，然后 A 和 B 在执行操作 4 时同时变空。
如果我们选择第三个操作，A 将在执行操作 [1, 2] 时变为空，然后 A 和 B 在执行操作 3 时同时变空。
如果我们选择第四个操作，A 将在执行操作 1 时变为空，然后 A 和 B 在执行操作 2 时同时变空。
所以 A 变为空的总概率加上 A 和 B 同时变为空的概率的一半是 0.71875。
 

提示:
0 <= n <= 10^9
*
*/
struct Solution {}

impl Solution {
    pub fn soup_servings(n: i32) -> f64 {
        if n >= 5000 {
            return 1.0;
        }        

        // 25的倍数. 这样可以减少计算遍历的数量
        let n = (n + 24) / 25;
        let mut memo: HashMap<(i32, i32), f64> = HashMap::new();


        fn dfs(a: i32, b: i32, memo: &mut HashMap<(i32, i32), f64>) -> f64 {
            if a <= 0 && b <= 0 {
                return 0.5;
            }
            if a <= 0 {
                return 1.0;
            }

            if b <= 0 {
                return 0.0;
            }

            if let Some(&res) = memo.get(&(a, b)) {
                return res;
            }
            
            let ans = 0.25 * (
                // a - 100, b - 0
                // a - 75, b - 25
                // a - 50, b - 50
                // a - 25, b - 75

                // 都是 25 的倍数，除以25
                // a - 4, b - 0
                // a - 3, b - 1
                // a - 2, b - 2
                // a - 1, b - 3
                dfs(a - 4, b, memo) + 
                dfs(a - 3, b - 1, memo) + 
                dfs(a - 2, b - 2, memo) + 
                dfs(a - 1, b - 3, memo) 
            
            );

            memo.insert((a, b), ans);
            ans
        }

        dfs(n, n, &mut memo)
    }


}

毫升 —> 带注释版

use std::collections::HashMap;

pub fn soup_servings(n: i32) -> f64 {
    // 根据题意，n 超过 4800 时，概率接近 1，直接返回 1.0 提前优化
    if n >= 4800 {
        return 1.0;
    }

    // 初始化记忆化搜索用的哈希表
    let mut memo = HashMap::new();

    // 开始 DFS，从 A 和 B 都是 n 单位（每单位代表 25 毫升）开始
    dfs(n, n, &mut memo)
}

// 记忆化 DFS 函数：参数为 A 汤剩余量、B 汤剩余量，以及记忆表
fn dfs(a: i32, b: i32, memo: &mut HashMap<(i32, i32), f64>) -> f64 {
    // 如果 A 和 B 都小于等于 0，表示同时耗尽，返回 0.5（按照题目要求）
    if a <= 0 && b <= 0 {
        return 0.5;
    }

    // 如果 A 耗尽但 B 还有，表示 A 先耗尽，返回 1.0
    if a <= 0 {
        return 1.0;
    }

    // 如果 B 耗尽但 A 还有，表示 B 先耗尽，返回 0.0
    if b <= 0 {
        return 0.0;
    }

    // 如果之前计算过 a, b 的结果，直接返回（避免重复计算）
    if let Some(&val) = memo.get(&(a, b)) {
        return val;
    }

    // 模拟 4 种操作，每种概率 0.25，累加期望
    let res = 0.25 * (
        dfs(a - 100, b, memo) +
        dfs(a - 75, b - 25, memo) +
        dfs(a - 50, b - 50, memo) +
        dfs(a - 25, b - 75, memo)
    );

    // 保存结果到备忘录
    memo.insert((a, b), res);

    res
}

网格类问题：题目是二维网格上的路径问题，常见解法包括DFS/BFS/动态规划。

路径探索：需要尝试所有可能的路径（而不是最短路径），优先考虑DFS。

不能重复访问单元格 → 需要回溯

题目要求从任意一个非零单元格出发，找到一条路径使得黄金总和最大，且路径不能重复访问单元格。 这种探索所有可能路径的问题通常可以用DFS来解决，因为：

DFS的特点：沿着一条路径一直走到底，直到无法继续，然后回溯尝试其他路径。

回溯的必要性：在DFS过程中，我们需要标记已访问的单元格，但在探索完一条路径后，必须撤销标记（回溯），否则会影响其他路径的探索。

关键点：

每个单元格只能被访问一次 → 需要 visited 数组标记。

可以从任意点出发 → 需要遍历所有非零单元格作为起点。

需要尝试所有可能的路径 → DFS天然适合。

AC Code

#![allow(unused_variables)]
#![allow(dead_code)]


/**
 *
你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。
每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

每当矿工进入一个单元，就会收集该单元格中的所有黄金。
矿工每次可以从当前位置向上下左右四个方向走。
每个单元格只能被开采（进入）一次。
不得开采（进入）黄金数目为 0 的单元格。
矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。
 

示例 1：
输入：grid = [[0,6,0],[5,8,7],[0,9,0]]
输出：24
解释：
[[0,6,0],
 [5,8,7],
 [0,9,0]]
一种收集最多黄金的路线是：9 -> 8 -> 7。


示例 2：
输入：grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出：28
解释：
[[1,0,7],
 [2,0,6],
 [3,4,5],
 [0,3,0],
 [9,0,20]]
一种收集最多黄金的路线是：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。
 

提示：
1 <= grid.length, grid[i].length <= 15
0 <= grid[i][j] <= 100
最多 25 个单元格中有黄金。
*
*/
struct Solution {}

impl Solution {
    pub fn get_maximum_gold(grid: Vec<Vec<i32>>) -> i32 {
        let mut ans = 0;

        let rows = grid.len();
        let cols = grid[0].len();

        let mut vis = vec![vec![false; cols]; rows];

        for i in 0..rows {
            for j in 0..cols {

                if grid[i][j] != 0 {
                    // 黄金
                    let current_gold = Self::dfs(&grid, &mut vis, i as i32, j as i32, rows as i32, cols as i32);

                    ans = ans.max(current_gold);
                }

            }
        }
        
        ans
    }


    fn dfs(grid: &Vec<Vec<i32>>, vis: &mut Vec<Vec<bool>>, i: i32, j: i32, rows: i32, cols: i32) -> i32 {

        if i < 0 || i >= rows || j < 0 || j >= cols || grid[i as usize][j as usize] == 0 || vis[i as usize][j as usize] == true {
            // 此路不通. 返回黄金 0 
            return 0;
        }

        vis[i as usize][j as usize] = true;
        let current = grid[i as usize][j as usize]; // 当前黄金价值
        let mut max_dir = 0;  // 最大价值的方向.

        // 定义四个方向 上下左右
        let dir: Vec<(i32, i32)> = vec![(0, 1), (0, -1), (-1, 0), (1, 0)];

        for (x, y) in dir {
            let next_x = i as i32 + x;
            let next_y = j as i32 + y;

            let next_glod = Self::dfs(grid, vis, next_x, next_y, rows, cols);

            max_dir = max_dir.max(next_glod);
        }

        // 还原
        vis[i as usize][j as usize] = false;

        current + max_dir
    } 
}

问题转换为：找到最长的子数组，其中最多只能包含两个不同的数字.

AC Code

#![allow(unused_variables)]
#![allow(dead_code)]

use std::collections::HashMap;

/**
 *
你正在探访一家农场，农场从左到右种植了一排果树。

这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。

采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。

 
示例 1：
输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。


示例 2：
输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。


示例 3：
输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。


示例 4：
输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：可以采摘 [1,2,1,1,2] 这五棵树。
 

提示：
1 <= fruits.length <= 10^5
0 <= fruits[i] < fruits.length
*
*/
struct Solution {}

impl Solution {
    pub fn total_fruit(fruits: Vec<i32>) -> i32 {
        let mut count = HashMap::new();
        let mut left = 0;


        let mut ans = 0 as i32;
        for right in 0..fruits.len() {
            *count.entry(fruits[right]).or_insert(0) += 1;

            while count.len() > 2 {
                let fruit = fruits[left];

                if let Some(&cnt) = count.get(&fruit) {
                    if cnt == 1 {
                        // 移除
                        count.remove(&fruit);
                    } else {
                        count.insert(fruit, cnt - 1);
                    }
                }

                left += 1;
            }


            ans = ans.max(right as i32 - left as i32 + 1);
        }
        
        ans
    }
}

方法思路

组合并排序工作：

首先将工作和对应的收益组合起来，然后按照工作的难度进行排序。这样我们可以按难度顺序处理工作。

预处理最大收益：

1.创建一个数组，其中每个位置记录到当前难度为止的最大收益。 2.这样，对于任意给定的工人能力，我们只需要找到不超过他能力的最大难度工作，并直接获取对应的最大收益。

排序工人能力：

将工人的能力排序，这样我们可以利用双指针技术或二分查找来高效地匹配工作和工人。

计算总收益：

对于每个工人，使用二分查找来确定他能完成的最大难度工作，并累加对应的最大收益。

#![allow(unused_variables)]
#![allow(dead_code)]

/**
 *
你有 n 个工作和 m 个工人。给定三个数组： difficulty, profit 和 worker ，其中:

difficulty[i] 表示第 i 个工作的难度，profit[i] 表示第 i 个工作的收益。
worker[i] 是第 i 个工人的能力，即该工人只能完成难度小于等于 worker[i] 的工作。
每个工人 最多 只能安排 一个 工作，但是一个工作可以 完成多次 。

举个例子，如果 3 个工人都尝试完成一份报酬为 $1 的同样工作，那么总收益为 $3 。
如果一个工人不能完成任何工作，他的收益为 $0 。
返回 在把工人分配到工作岗位后，我们所能获得的最大利润 。



示例 1：

输入: difficulty = [2,4,6,8,10], profit = [10,20,30,40,50], worker = [4,5,6,7]
输出: 100
解释: 工人被分配的工作难度是 [4,4,6,6] ，分别获得 [20,20,30,30] 的收益。
示例 2:

输入: difficulty = [85,47,57], profit = [24,66,99], worker = [40,25,25]
输出: 0


提示:

n == difficulty.length
n == profit.length
m == worker.length
1 <= n, m <= 10^4
1 <= difficulty[i], profit[i], worker[i] <= 10^5
*
*/
struct Solution {}

impl Solution {
    pub fn max_profit_assignment(difficulty: Vec<i32>, profit: Vec<i32>, worker: Vec<i32>) -> i32 {
        // 组合难度 和 收益
        // 按难度排序
        // 遍历有序难度，记录最大收益

        // 遍历工人难度，二分查找能得到的最大收益

        let len = difficulty.len();
        let mut jobs: Vec<(i32, i32)> = difficulty.into_iter().zip(profit.into_iter()).collect();

        // 重点！！！！ 排序
        jobs.sort_by(|a, b| a.0.cmp(&b.0));

        let mut max_profit_up_to = Vec::with_capacity(len);
        let mut current_max_profit = 0;

        // for &job in &jobs {
        //     current_max_profit = current_max_profit.max(job.1);
        for &(_, p) in &jobs {
            current_max_profit = current_max_profit.max(p);
            max_profit_up_to.push(current_max_profit);
        }

        let mut ans = 0;

        for w in worker {
            let mut left = 0;
            let mut right = max_profit_up_to.len();
            while left < right {
                let mid = left + (right - left) / 2;

                // <= 是第一个大于 w 的idx
                // < 是第一个大于等于 w 的idx
                if jobs[mid].0 <= w {
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }

            // left ==> 第一个大于 w  的idx
            // left - 1 ===> 就是第一个 <= worker 难度的
            if left > 0 {
                ans += max_profit_up_to[left - 1];
            }
        }

        ans
    }
}

回溯法：由于n的范围较小（1 <= n <= 20），可以使用回溯法来尝试所有可能的序列构造方式。

字典序最大： 为了确保字典序最大，我们应优先尝试较大的数字。因此，在回溯过程中，从大到小尝试放置数字。

条件检查： 在放置数字时，需要检查当前数字是否已经放置过 （对于1，只能放置一次；对于其他数字，最多放置两次），并且两个相同数字i之间的距离必须恰好为i。

#![allow(unused_variables)]
#![allow(dead_code)]

use std::task::Context;

/**
 *
给你一个整数 n ，请你找到满足下面条件的一个序列：

整数 1 在序列中只出现一次。
2 到 n 之间每个整数都恰好出现两次。
对于每个 2 到 n 之间的整数 i ，两个 i 之间出现的距离恰好为 i 。
序列里面两个数 a[i] 和 a[j] 之间的 距离 ，我们定义为它们下标绝对值之差 |j - i| 。

请你返回满足上述条件中 字典序最大 的序列。题目保证在给定限制条件下，一定存在解。

一个序列 a 被认为比序列 b （两者长度相同）字典序更大的条件是：
a 和 b 中第一个不一样的数字处，a 序列的数字比 b 序列的数字大。比方说，[0,1,9,0] 比 [0,1,5,6] 字典序更大，
因为第一个不同的位置是第三个数字，且 9 比 5 大。



示例 1：
输入：n = 3
输出：[3,1,2,3,2]
解释：[2,3,2,1,3] 也是一个可行的序列，但是 [3,1,2,3,2] 是字典序最大的序列。



示例 2：
输入：n = 5
输出：[5,3,1,4,3,5,2,4,2]


提示：
1 <= n <= 20
*
*/
struct Solution {}

impl Solution {
    pub fn construct_distanced_sequence(n: i32) -> Vec<i32> {
        let len = n as usize;
        let mut ans = vec![0; 2 * len - 1];
        // 记录数字是否被使用 1..=n
        let mut used = vec![false; len + 1];

        Self::backtrace(&mut ans, &mut used, len, 0);

        ans
    }

    /// 核心思路：两个数字一起放.
    fn backtrace(ans: &mut Vec<i32>, used: &mut Vec<bool>, len: usize, idx: usize) -> bool {
        // 终止条件 ans 所有位置都已填满
        if idx == ans.len() {
            return true;
        }

        // 判断当前位置是否已经用过了
        if ans[idx] != 0 {
            // 下一个位置
            return Self::backtrace(ans, used, len, idx + 1);
        }

        // 放入数字 从大到小，确保字典序最大
        for n in (1..=len).rev() {
            if used[n] {
                continue;
            }
            // 分情况讨论
            // 如果 n  == 1， 只插入一次
            if n == 1 {
                ans[idx] = 1;
                used[1] = true;

                // 下一个位置
                if Self::backtrace(ans, used, len, idx + 1) {
                    return true; // 放置成功，返回true退出
                }

                // 回溯
                ans[idx] = 0;
                used[1] = false;
            } else {
                // 检查位置是否可用
                if idx + n >= ans.len() || ans[idx + n] != 0 {
                    continue ;
                }

                // n >= 2 ，插入两次
                ans[idx] = n as i32;
                ans[idx + n] = n as i32;
                used[n] = true;

                // 处理下一个位置
                if Self::backtrace(ans, used, len, idx + 1) {
                    return true; // 放置成功，返回true退出
                }
                // 放置失败，走下面回溯尝试其他

                // 回溯
                ans[idx] = 0;
                ans[idx + n] = 0;
                used[n] = false;
            }
        }

        false
    }
}

方法思路 问题分析： 我们需要从起始位置startPos出发，可以向左或向右移动，总步数不超过k。 每次移动到一个位置，可以摘取该位置的所有水果。目标是最大化摘取的水果数量。

关键观察：

最优路径通常由以下几种情况组成：

1. 一直向右移动。

2. 一直向左移动。

3. 先向左移动一定距离，再向右移动。

4. 先向右移动一定距离，再向左移动。

对于每种情况，我们需要计算在k步内能够覆盖的区间，并统计该区间内的水果总数。

滑动窗口：

我们可以使用滑动窗口技术来高效地计算在某个区间内的水果总数。具体步骤如下：

预处理水果的位置和数量，存储在一个数组中，并计算前缀和数组，以便快速查询区间和。

枚举所有可能的左右移动组合。 例如，对于左移 l 步和右移 r 步，满足 l + r + min(l, r) <= k（因为来回移动需要额外的步数）。

使用二分查找来确定在某个区间内的水果位置，并利用前缀和数组快速求和。

其他：

if let 复习

if let Ok(idx) = result {
    // 如果匹配 Ok(idx)，执行这里
} else {
    // 如果匹配 Err 或其他情况，执行这里
}

AC Code 如下

#![allow(unused_variables)]
#![allow(dead_code)]

/**
 *
在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。
给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。
fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。
从任何位置，你可以选择 向左或者向右 走。
在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。
你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

 
示例 1：
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：
- 向右移动到位置 6 ，摘到 3 个水果
- 向右移动到位置 8 ，摘到 6 个水果
移动 3 步，共摘到 3 + 6 = 9 个水果


示例 2：
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：
- 在初始位置 5 ，摘到 7 个水果
- 向左移动到位置 4 ，摘到 1 个水果
- 向右移动到位置 6 ，摘到 2 个水果
- 向右移动到位置 7 ，摘到 4 个水果
移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果


示例 3：
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方
 

提示：
1 <= fruits.length <= 10^5
fruits[i].length == 2
0 <= startPos, positioni <= 2 * 10^5
对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0 开始计数）
1 <= amounti <= 10^4
0 <= k <= 2 * 10^5
*
*/
pub fn max_total_fruits(fruits: Vec<Vec<i32>>, start_pos: i32, k: i32) -> i32 {
    // 初始化
    // 记录前缀和、水果位置 -- 用于快速计算区间和
    let len = fruits.len();
    let mut prefix_sum = Vec::new();
    let mut positions = Vec::new();
    
    prefix_sum.push(0);

    for f in &fruits {
        positions.push(f[0]);
        prefix_sum.push(prefix_sum.last().unwrap() + f[1]);
    }


    let mut ans = 0;

    // 起始位置
    let start = start_pos;
    let k = k;

    // 特殊情况
    if k == 0 {
        if let Ok(idx) = positions.binary_search(&start) {
            return fruits[idx][1];
        } else {
            return 0;
        }
    }

    // 情况1
    // 先向左走l步，然后剩余步数向右走
    for l in 0..k {
        // 剩余步数 l + r + l <= k (因为先左后右，需要返回)
        let r = k - 2 * l;
        if r < 0 {
            continue ; // 如果r为负数. 跳过
        }
        // 能到达的最远区间位置
        let current_left = start - l;
        let current_right = start + r;

        // 【二分差找】 确认current_left 和 current_right 在 position 中的位置
        let left_idx = match positions.binary_search(&current_left) {
            Ok(idx) => idx,  // 找到该位置，默认返回的是 current_left 插入位置. 即 positions[current_left] <= positions[idx]
            Err(idx) => idx, // 未找到.
        };

        let right_idx = match positions.binary_search(&current_right) {
            Ok(idx) => idx,  // 找到该位置，即 positions[current_right] <= positions[idx]
            Err(idx) => idx - 1, // 未找到，即 positions[current_right] >= positions[idx - 1]
        };

        // 计算水果
        if left_idx <= right_idx && right_idx < positions.len() {
            // prefix_sum[right_idx + 1] 就是 right_idx 之和. prefix_sum[0] = 0
            let sum = prefix_sum[right_idx + 1] - prefix_sum[left_idx];
            ans = ans.max(sum); 
        }
    }




    // 情况2
    // 先向右走r步，然后剩余部署向左走
    for r in 0..k {
        // r + l + r <= k
        let l = k - 2 * r;

        let current_left = start - l;
        let current_right = start + r;

        // 二分差找
        let left_idx = match positions.binary_search(&current_left) {
            Ok(idx) => idx, 
            Err(idx) => idx,
        };

        let right_idx = match positions.binary_search(&current_right) {
            Ok(idx) => idx, 
            Err(idx) => idx - 1,
        };

        if left_idx <= right_idx && right_idx < positions.len() {
            let sum = prefix_sum[right_idx + 1] - prefix_sum[left_idx];
            ans = ans.max(sum);
        }
    }

    ans
}

带注释版 AC code

pub fn max_total_fruits(fruits: Vec<Vec<i32>>, start_pos: i32, k: i32) -> i32 {
    let n = fruits.len();
    let mut prefix_sum = Vec::new(); // 前缀和数组，用于快速计算区间和
    let mut positions = Vec::new();  // 存储所有水果的位置

    // 初始化前缀和数组，第一个元素为0
    prefix_sum.push(0);
    // 遍历水果数组，填充positions和prefix_sum
    for fruit in &fruits {
        positions.push(fruit[0]); // 存储水果位置
        prefix_sum.push(prefix_sum.last().unwrap() + fruit[1]); // 计算前缀和
    }

    let mut best = 0; // 记录最大水果总数

    let start = start_pos; // 起始位置
    let k = k; // 最大步数

    // 特殊情况，k==0
    if k == 0 {
        if let Ok(idx) = positions.binary_search(&start) {
            return fruits[idx][1];
        } else {
            return 0;
        }
    }

    // 情况1：先向左走l步，再向右走r步，满足 l + r + min(l, r) <= k
    // 这里等价于 l + r + l <= k （因为先左后右，需要返回）
    // 所以 r = k - 2*l
    for l in 0..=k {
        let r = k - 2 * l; // 剩余的步数用于向右走
        if r < 0 {
            continue; // 如果r为负数，跳过
        }
        let current_left = start - l; // 向左走到的最远位置
        let current_right = start + r; // 向右走到的最远位置

        // 使用二分查找确定current_left在positions中的位置
        let left_idx = match positions.binary_search(&current_left) {
            Ok(idx) => idx, // 找到该位置
            Err(idx) => idx, // 未找到，返回插入位置
        };
        // 使用二分查找确定current_right在positions中的位置
        let right_idx = match positions.binary_search(&current_right) {
            Ok(idx) => idx, // 找到该位置
            Err(idx) => idx - 1, // 未找到，返回前一个位置
        };

        // 检查left_idx和right_idx是否有效，并计算区间和
        if left_idx <= right_idx && right_idx < positions.len() {
            let sum = prefix_sum[right_idx + 1] - prefix_sum[left_idx];
            if sum > best {
                best = sum; // 更新最大水果总数
            }
        }
    }

    // 情况2：先向右走r步，再向左走l步，满足 r + l + min(r, l) <= k
    // 这里等价于 r + l + r <= k （因为先右后左，需要返回）
    // 所以 l = k - 2*r
    for r in 0..=k {
        let l = k - 2 * r; // 剩余的步数用于向左走
        if l < 0 {
            continue; // 如果l为负数，跳过
        }
        let current_right = start + r; // 向右走到的最远位置
        let current_left = start - l; // 向左走到的最远位置

        // 使用二分查找确定current_left在positions中的位置
        let left_idx = match positions.binary_search(&current_left) {
            Ok(idx) => idx, // 找到该位置
            Err(idx) => idx, // 未找到，返回插入位置
        };
        // 使用二分查找确定current_right在positions中的位置
        let right_idx = match positions.binary_search(&current_right) {
            Ok(idx) => idx, // 找到该位置
            Err(idx) => idx - 1, // 未找到，返回前一个位置
        };

        // 检查left_idx和right_idx是否有效，并计算区间和
        if left_idx <= right_idx && right_idx < positions.len() {
            let sum = prefix_sum[right_idx + 1] - prefix_sum[left_idx];
            if sum > best {
                best = sum; // 更新最大水果总数
            }
        }
    }

    best // 返回最大水果总数
}